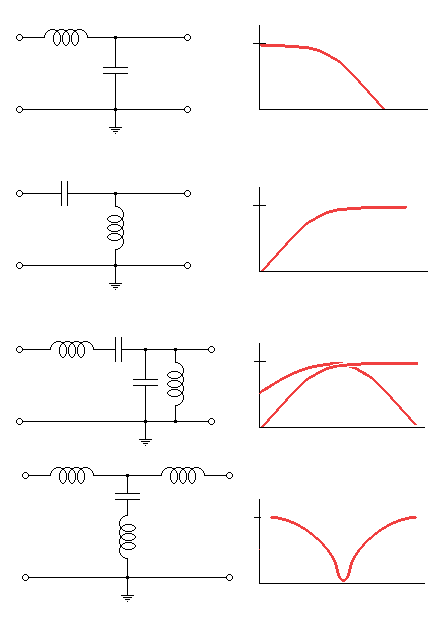
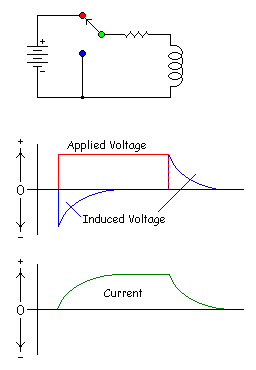
When
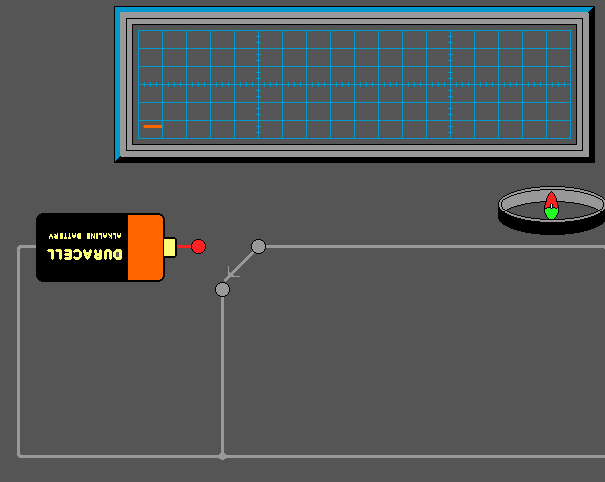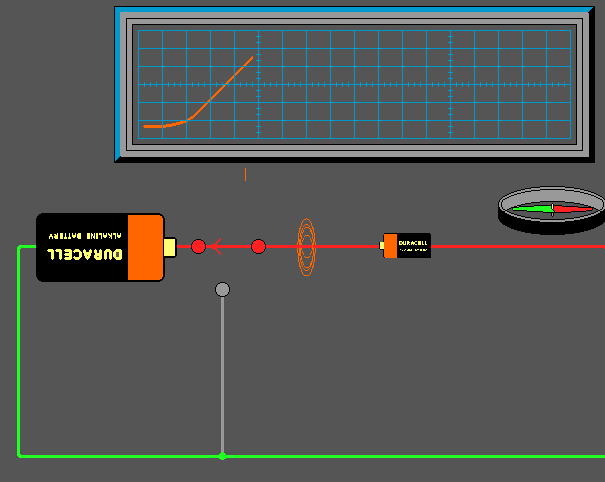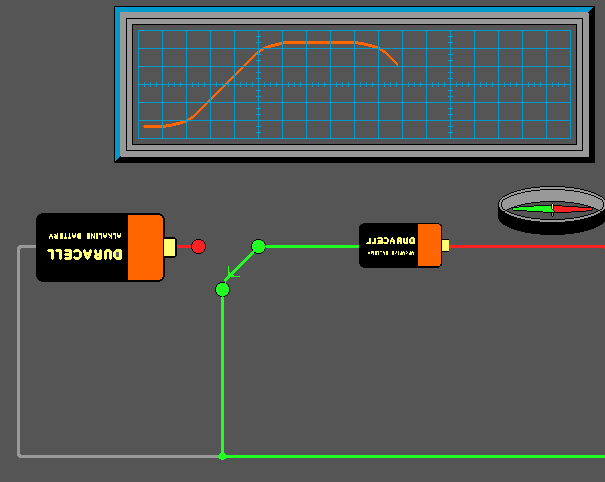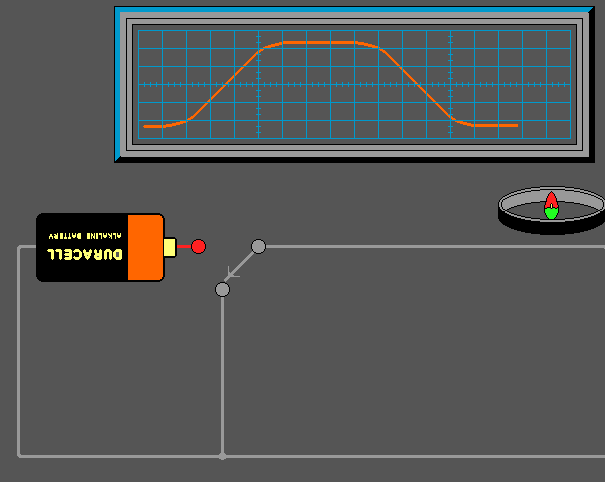
a Voltage (step function) is applied to an Inductor, a current is made
to flow through its conductors creating an expanding Magnetic Field (Flux).
| This expanding Field induces a current (Counter
E.M.F.) possessing an opposite polarity from that of the applied voltage.
The amount of this counter E.M.F. is directly related to the derivative
of the applied current, i.e., the faster the rise/fall the greater the
current. The effect of this is to impede the rate of expansion of
the Magnetic field.
Next, the Magnetic
field stops expanding and becomes steady-state. At this point the Inductor
is now only a Resistive load to the applied Voltage Source.
Finally, the
applied voltage is removed--made to equal Zero (Vapplied
= 0 volts); the steady-state Magnetic Field now starts to collapse, which
induces an E.M.F into the inductor thus causing a Current to flow (of the
same polarity as that of the original applied voltage source). As in the
applied case there is a Counter E.M.F. generated by the Current
generated from the collapsing Magnetic Field, again impeding the collapse
of said Magnetic Field. |
|
|
The
transfer of energy to the magnetic field of an inductor represents work
performed by the source of the voltage. Power is required for doing the
work, and since power is equal to Current multiplied by Voltage, there
must be a voltage drop in the circuit while energy is being stored in the
field. This voltage drop, exclusive of any voltage caused by the resistance
(IR drop) in the circuit, is the result of an opposing voltage induced
in the circuit while the field is building up to its final value.
Once the field becomes constant, the induced voltage or back-voltage
disappears, because no further energy is being stored. The induced voltage
opposes the voltage of the source and tends to prevent the current from
rising rapidly when the circuit is closed. The amplitude of the induced
voltage is proportional to the rate at which the current changes (and consequently
the
rate at which the magnetic field changes) and to a constant associated
with the circuit itself: the inductance (or self-inductance) of the circuit. |
 |
|
| The effect that an Inductance has on Impeding current
flow (due to the derivative of the applied current & the Inductance--measured
in
Henrys) is analogous to the Effect of Resistance on impeding
current flow in a D.C. Circuit. However, this is a Reactive Impedance (Z);
in this case Inductive Reactance (XL) measured in Ohms (Z =
XL). |
| From the above, one can imagine if the Rate at which the applied
voltage were fast enough, even a short piece of wire could exhibit relatively
high impedances. --And they Do!
See
Bypassing
& Decoupling
|
|